Omgfare

What are the odds? As a poker player, that’s the first thing you should ask. Here some key numbers to get your play off the ground.

The chances of getting a top starting hand (of double aces, picture pairs or A-K suited), is a minute 2.1%. Hold out for one of these and you’ll never get started.

If you've got a flush draw (one card short of a full flush) after the flop, you'll make your hand 34.97% of the time. That's just over a third.

The odds of flopping a flush when you have two suited cards is 1 in 118, but even when you do flop a flush, you have to be careful that your flush holds up for the rest of the hand. Any player with a higher card of the same suit as your flush has a little more than a 2:1 chance of hitting another card on the turn or river to beat you. If you flop an open-ended straight draw this gives you eight outs (eight possible cards that will complete the hand), so you'll hit your hand by the river 31.5% of the time. Just make sure you're getting pot odds (the value of the pot versus the value of your bet) to see the next card. Flopping a pair. 32.43% are the chances of making a pair on the flop. That doesn’t mean you should be playing any two cards, as the same odds apply for players with a higher hole cards. On a flush draw! Your chances of making a flush after the flop when on a flush draw are at 34.97%! It’s a great feeling when you’re on a flush draw on the.

Don't play any two cards just because they're suited. It only improves your hand by 2.5%.

The chance of one of your hole cards making a pair on the flop is 32.43%, or about a third.

By the river, your chances of making a pair go up to roughly a half.

If you flop an open-ended straight draw this gives you eight outs (eight possible cards that will complete the hand), so you'll hit your hand by the river 31.5% of the time. Just make sure you're getting pot odds (the value of the pot versus the value of your bet) to see the next card.

If you already have a pair, the odds of flopping a set (three of a kind) are only 7.5/1 – so make sure you only play small pairs cheaply, and only if the pot is worth it.

Rarely worth drawing to, with the turn and river cards to come you'll hit your gutshot straight (four outs) approximately 9% of the time.

When two pairs go head to head, the bigger pair will win roughly 80% of the time (or four times out of five). So if you’ve got queens, and see a bet, raise and re-raise in front of you, you might be up against aces, kings, or possibly both. Time to fold.

If you need two exact cards on the turn and river, the chance of getting them both is only 0.3%. If you get one, there's a 4.55% chance of getting the other.

A pair against two overcards is often called a coin-flip or race, because they each win about half the time. If the overcards are suited, the pair will win 46%-54% of the time, if not, 48%-57% of the time.

If your top card matches the other person's, but your kicker is smaller (for example, queen against either ace or king, you’ve only got a 24% chance of winning (or about one in four).

People talk about middle suited connectors being better than aces, because of the straight and flush possibilities. But if you're holding the aces, don't panic – the over-pair will beat the suited connectors approximately 80% of the time.

It might not feel like it, but you'll be dealt a pocket pair on average once every 17 hands, or about 6% of the time.

There's a reason for folding low hands. Even if they’re suited, the chance of flopping a flush is only 0.8% – or 124/1.

The probability of flopping two-pair (from non-paired hole cards) is about 2%.

If you do get two pair on the flop, the chances of making at least a full house by the river is 16.74%.

But if you flop three-of-a-kind, the odds of making a full house or better by the river go up to 33.4%, or one in three.

You bluffed with random cards to steal the blinds and were called by A-K. Oops! Actually, your random lower cards will win about 35% of the time.

Pocket jacks is known as a big danger hand in Texas Hold’em. It may look good, but the chances of a higher card turning up on the flop is 52%, giving your ‘fish-hooks’ less than half a chance of survival.

In our poker math and probability lesson it was stated that when it comes to poker; “the math is essential“. Although you don’t need to be a math genius to play poker, a solid understanding of probability will serve you well and knowing the odds is what it’s all about in poker. It has also been said that in poker, there are good bets and bad bets. The game just determines who can tell the difference. That statement relates to the importance of knowing and understanding the math of the game.

In this lesson, we’re going to focus on drawing odds in poker and how to calculate your chances of hitting a winning hand. We’ll start with some basic math before showing you how to correctly calculate your odds. Don’t worry about any complex math – we will show you how to crunch the numbers, but we’ll also provide some simple and easy shortcuts that you can commit to memory.

Basic Math – Odds and Percentages

Odds can be expressed both “for” and “against”. Let’s use a poker example to illustrate. The odds against hitting a flush when you hold four suited cards with one card to come is expressed as approximately 4-to-1. This is a ratio, not a fraction. It doesn’t mean “a quarter”. To figure the odds for this event simply add 4 and 1 together, which makes 5. So in this example you would expect to hit your flush 1 out of every 5 times. In percentage terms this would be expressed as 20% (100 / 5).

Here are some examples:

• 2-to-1 against = 1 out of every 3 times = 33.3%
• 3-to-1 against = 1 out of every 4 times = 25%
• 4-to-1 against = 1 out of every 5 times= 20%
• 5-to-1 against = 1 out of every 6 times = 16.6%

Converting odds into a percentage:

• 3-to-1 odds: 3 + 1 = 4. Then 100 / 4 = 25%
• 4-to-1 odds: 4 + 1 = 5. Then 100 / 5 = 20%

Converting a percentage into odds:

• 25%: 100 / 25 = 4. Then 4 – 1 = 3, giving 3-to-1 odds.
• 20%: 100 / 20 = 5. Then 5 – 1 = 4, giving 4-to-1 odds.

Another method of converting percentage into odds is to divide the percentage chance when you don’t hit by the percentage when you do hit. For example, with a 20% chance of hitting (such as in a flush draw) we would do the following; 80% / 20% = 4, thus 4-to-1. Here are some other examples:

• 25% chance = 75 / 25 = 3 (thus, 3-to-1 odds).
• 30% chance = 70 / 30 = 2.33 (thus, 2.33-to-1 odds).

Some people are more comfortable working with percentages rather than odds, and vice versa. What’s most important is that you fully understand how odds work, because now we’re going to apply this knowledge of odds to the game of poker.

DO YOU PLAY TOURNAMENTS?

One of the most vital skills you can have is knowing when, and when not, to 3bet all-in preflop. Preflop aggression is crucial in middle-late stages, and this Crash Course will prepare you to 3bet like a pro from EVERY position. Stop guessing, start crushing, and 3bet your way to the final table.

Counting Your Outs

Before you can begin to calculate your poker odds you need to know your “outs”. An out is a card which will make your hand. For example, if you are on a flush draw with four hearts in your hand, then there will be nine hearts (outs) remaining in the deck to give you a flush. Remember there are thirteen cards in a suit, so this is easily worked out; 13 – 4 = 9.

Another example would be if you hold a hand like and hit two pair on the flop of . You might already have the best hand, but there’s room for improvement and you have four ways of making a full house. Any of the following cards will help improve your hand to a full house; .

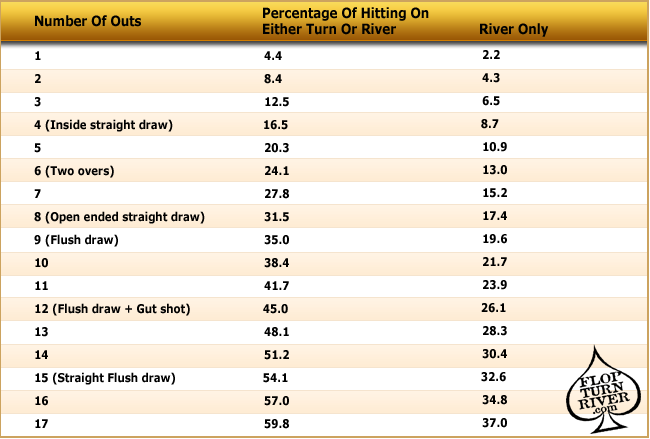
The following table provides a short list of some common outs for post-flop play. I recommend you commit these outs to memory:

Table #1 – Outs to Improve Your Hand

The next table provides a list of even more types of draws and give examples, including the specific outs needed to make your hand. Take a moment to study these examples:

Table #2 – Examples of Drawing Hands (click to enlarge)

Counting outs is a fairly straightforward process. You simply count the number of unknown cards that will improve your hand, right? Wait… there are one or two things you need to consider:

Don’t Count Outs Twice

There are 15 outs when you have both a straight and flush draw. You might be wondering why it’s 15 outs and not 17 outs, since there are 8 outs to make a straight and 9 outs for a flush (and 8 + 9 = 17). The reason is simple… in our example from table #2 the and the will make a flush and also complete a straight. These outs cannot be counted twice, so our total outs for this type of draw is 15 and not 17.

Anti-Outs and Blockers

There are outs that will improve your hand but won’t help you win. For example, suppose you hold on a flop of . You’re drawing to a straight and any two or any seven will help you make it. However, the flop also contains two hearts, so if you hit the or the you will have a straight, but could be losing to a flush. So from 8 possible outs you really only have 6 good outs.

It’s generally better to err on the side of caution when assessing your possible outs. Don’t fall into the trap of assuming that all your outs will help you. Some won’t, and they should be discounted from the equation. There are good outs, no-so good outs, and anti-outs. Keep this in mind.

Calculating Your Poker Odds

Once you know how many outs you’ve got (remember to only include “good outs”), it’s time to calculate your odds. There are many ways to figure the actual odds of hitting these outs, and we’ll explain three methods. This first one does not require math, just use the handy chart below:

Table #3 – Poker Odds Chart

As you can see in the above table, if you’re holding a flush draw after the flop (9 outs) you have a 19.1% chance of hitting it on the turn or expressed in odds, you’re 4.22-to-1 against. The odds are slightly better from the turn to the river, and much better when you have both cards still to come. Indeed, with both the turn and river you have a 35% chance of making your flush, or 1.86-to-1.

We have created a printable version of the poker drawing odds chart which will load as a PDF document (in a new window). You’ll need to have Adobe Acrobat on your computer to be able to view the PDF, but this is installed on most computers by default. We recommend you print the chart and use it as a source of reference. It should come in very handy.

Doing the Math – Crunching Numbers

There are a couple of ways to do the math. One is complete and totally accurate and the other, a short cut which is close enough.

Let’s again use a flush draw as an example. The odds against hitting your flush from the flop to the river is 1.86-to-1. How do we get to this number? Let’s take a look…

With 9 hearts remaining there would be 36 combinations of getting 2 hearts and making your flush with 5 hearts. This is calculated as follows:

(9 x 8 / 2 x 1) = (72 / 2) ≈ 36.

This is the probability of 2 running hearts when you only need 1 but this has to be figured. Of the 47 unknown remaining cards, 38 of them can combine with any of the 9 remaining hearts:

Poker Odds Of Flopping A Flush Drawings

9 x 38 ≈ 342.

Now we know there are 342 combinations of any non heart/heart combination. So we then add the two combinations that can make you your flush:

36 + 342 ≈ 380.

The total number of turn and river combos is 1081 which is calculated as follows:

(47 x 46 / 2 x 1) = (2162 / 2) ≈ 1081.

Now you take the 380 possible ways to make it and divide by the 1081 total possible outcomes:

380 / 1081 = 35.18518%

This number can be rounded to .352 or just .35 in decimal terms. You divide .35 into its reciprocal of .65:

0.65 / 0.35 = 1.8571428

And voila, this is how we reach 1.86. If that made you dizzy, here is the short hand method because you do not need to know it to 7 decimal points.

The Rule of Four and Two

A much easier way of calculating poker odds is the 4 and 2 method, which states you multiply your outs by 4 when you have both the turn and river to come – and with one card to go (i.e. turn to river) you would multiply your outs by 2 instead of 4.

Imagine a player goes all-in and by calling you’re guaranteed to see both the turn and river cards. If you have nine outs then it’s just a case of 9 x 4 = 36. It doesn’t match the exact odds given in the chart, but it’s accurate enough.

What about with just one card to come? Well, it’s even easier. Using our flush example, nine outs would equal 18% (9 x 2). For a straight draw, simply count the outs and multiply by two, so that’s 16% (8 x 2) – which is almost 17%. Again, it’s close enough and easy to do – you really don’t have to be a math genius.

Do you know how to maximize value when your draw DOES hit? Like…when to slowplay, when to continue betting, and if you do bet or raise – what the perfect size is? These are all things you’ll learn in CORE, and you can dive into this monster course today for just $5 down…

Conclusion

In this lesson we’ve covered a lot of ground. We haven’t mentioned the topic of pot odds yet – which is when we calculate whether or not it’s correct to call a bet based on the odds. This lesson was step one of the process, and in our pot odds lesson we’ll give some examples of how the knowledge of poker odds is applied to making crucial decisions at the poker table.

As for calculating your odds…. have faith in the tables, they are accurate and the math is correct. Memorize some of the common draws, such as knowing that a flush draw is 4-to-1 against or 20%. The reason this is easier is that it requires less work when calculating the pot odds, which we’ll get to in the next lesson.

Odds Of A Flush

By Tom 'TIME' Leonard

Tom has been writing about poker since 1994 and has played across the USA for over 40 years, playing every game in almost every card room in Atlantic City, California and Las Vegas.